红黑树的原理
这红黑树真是有毒,看了我好几天才大致搞清楚它在干嘛,原理什么的还迷迷糊糊。
二叉排序树
二叉排序树大家应该比较熟悉了,就是一个二叉树,左孩子的值比父节点小,右孩子比父节点大。但是二叉排序树在插入和删除过程中容易导致树失去平衡,导致查找效率降低。而红黑树就是平衡二叉树的一种实现方法。
红黑树
既然红黑树就是平衡二叉树的一种实现方法,那红黑树就是一颗二叉排序树,拥有二叉排序树的全部特性。除此以外,红黑树还有五条规则:
每个节点要么是红色,要么是黑色
根节点永远是黑色
所有的叶节点都是是黑色的(注意这里说叶子节点其实是上图中的 NIL 节点)
每个红色节点的两个子节点一定都是黑色(从每个叶子到根的所有路径上不能有两个连续的红色节点)
从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点

粗略的说,红黑树添加节点和删除节点都是分两部,第一步是先把数据插入/删除数据,由于插入/删除可能导致新的树不符合红黑树的规则,所以第二步是在以及插入/删除的新树上通过旋转或者修改节点的颜色来把新树调整回符合规则。
红黑树的旋转
红黑树的旋转除了调整节点之间的父子关系以外,由于节点还有颜色,所以还需要加一步对颜色的修改。下面这两个动图演示的只是节点间的关系的改变,而颜色的修改方法是:左旋和右旋都是E和S两个节点对调,E和S之间的颜色也要对调,当然颜色一样就不需要了。下文关于红黑树的旋转都是包活颜色上的对调的。
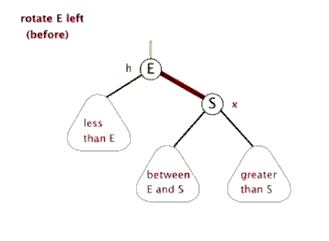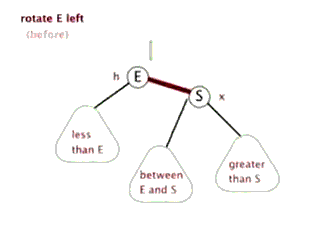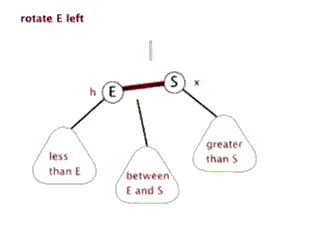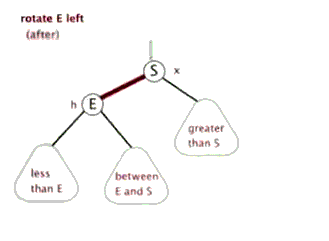
> 左旋
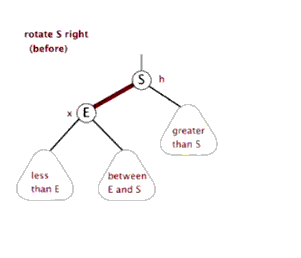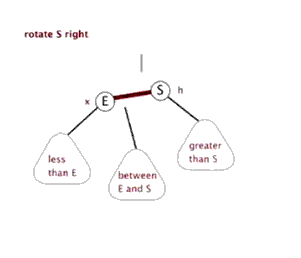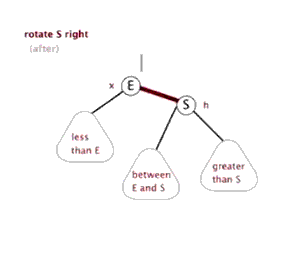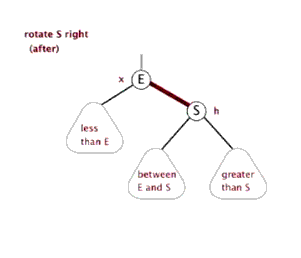
> 右旋
红黑树的插入
第一步,如上所说,先把数据插入进树再说。既然红黑树是二叉排序树,那么插入位置的确定就是按二叉排序树的插入 方法,这里就不多说了。选择好插入位置之后,还有一个问题没解决,那就是这个新插入的节点是红色还是黑色?一般都是把新插入的节点颜色设置为红色的,这样会使得违反红黑树规则的情况简单一点。那么插入一个红色节点什么情况下会导致违反规则而需要调整树呢?
第二步,当新插入的红色节点的父节点也是红色就违反了规则了。同时由于父亲节点是红色,所以爷爷节点一定是黑色。对树的调整还需要考虑其叔叔节点的颜色,黑色的爷爷节点叔叔节点颜色并不确定,所以这里要做个分类讨论。
叔叔节点是红色
节点N是新插入的,如果叔叔是红色,那么爷爷节点就肯定是黑色。这种情况需要把父亲和叔叔改为黑色,把爷爷改为红色。解决了两个红色相连的问题。但是爷爷变红色的,如果爷爷的父节点也是红色怎么办,所以这里需要进行递归,把爷爷节点当做是新插入的节点做调整,最后到根节点一定是黑色,所以一定会停下来。
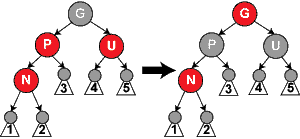
> 图1叔叔节点是黑色
把P和G进行旋转。
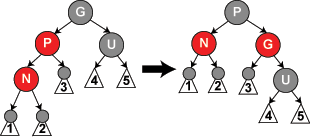
> 图2还有一直情况,上面新插入的是左孩子,如果是右孩子的话,跟父节点旋转转换,就变成是左孩子的情况了。
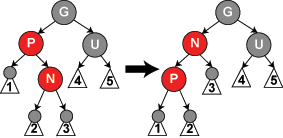
> 图3
红黑树的删除
如上,第一步,先把数据从树里删除。(基础不牢啊,并没有接触过二叉排序树的怎么删除的,花了好多时间在这里理解,看了好几个博客,最后对比着连蒙带猜得到下面的说法)对于二叉排序树而言,删除某个节点可以转换为删除另一个最多只有一个孩子的节点,这个孩子节点还是叶子节点。这有啥用呢?干嘛的呢?思路这样的:例如图3,要删除G节点的数据,但是我不删除G节点,我找G节点的左子树里值最大的那个值赋值到G节点了,即N节点,即符合二叉排序树的规则,也把G本来的数据给移除了。那么问题就转换为删除N节点了。这样做有什么好处,为什么不直接删除G节点,还要这样换来换去?对于删除任意一个节点,这个节点可能没有孩子,可能有一个孩子,可能有两个孩子,0和1个孩子的情况,直接把null/孩子替换指针就好。但是有两个孩子问题就难办了。但是,换为删除左子树里值最大的那个节点,这个节点最多只有一个孩子的节点,就避开了有两个孩子的问题了。然后,又要根据N的孩子数进行分类讨论了:
N没有孩子
直接删除NN有一个孩子
很遗憾,这次又不是直接删除N,是把N的孩子的值赋到N里,把N的孩子删掉。至于为什么要这么做,后面会讲到。
第二步,删除节点后调整红黑关系。实际上,删除的是节点N或者节点N的孩子,所以节点N可能还存在或者已经是null了,下面为了叙述方便,把null和N节点还存在的情况都叫做节点N。null也没所谓,因为调整过程它只会被别人引用。调整过程需要考虑N的父亲节点,兄弟节点以及兄弟节点的孩子的颜色情况,情况比较复杂,继续分类讨论:先分类父亲节点和兄弟节点的颜色,按排列组合有四种情况,但是由于父亲节点和兄弟节点都是红色是不存在的,所以实际上只有三种。
- 父亲节点是黑色,兄弟节点是黑色
下一步,以兄弟节点孩子SL和SR的颜色进行进一步的分类讨论SL和SR都是黑色的。把S颜色改为红色。由于P的左子树和右子树都少了一个黑色,所以经过P的相比于其他就少了一个黑色,破坏了红黑树规则,P的情况就像一开始N一样,经过N的都少了一个黑色,所以用递归的方法对P进行同样的处理。
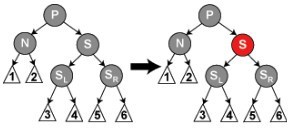
SL是红色,SR是黑色。把SL与S进行旋转,把这种情况转变成第三种情况
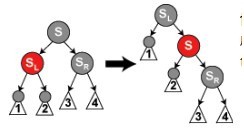
SL是任意颜色,SR是红色。把P和S进行旋转,再把SR颜色改为黑色即可。
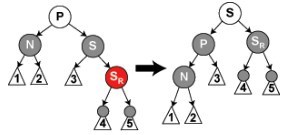
- 父亲节点是黑色,兄弟节点是红色
- SL和SR都是黑色(只有这种可能了,情况比较简单)把P和S进行旋转(我的理解这样即可,但是网上说还要按什么什么情况来继续操作)
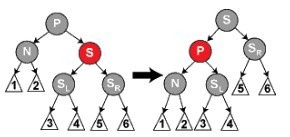
- SL和SR都是黑色(只有这种可能了,情况比较简单)把P和S进行旋转(我的理解这样即可,但是网上说还要按什么什么情况来继续操作)
- 父亲节点是红色,兄弟节点是黑色
父亲节点是红色,兄弟节点是黑色跟父亲节点是黑色,兄弟节点是黑色相似。
红黑树好迷,又复杂,不是很想实现。
参考文献