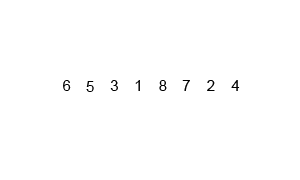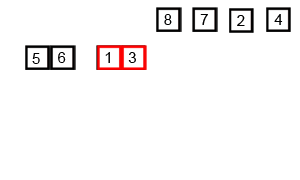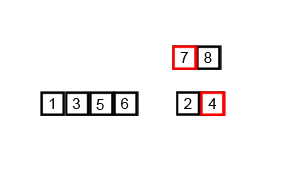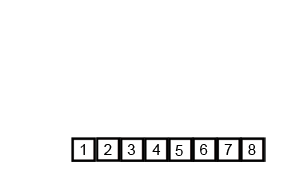数据结构与八大排序算法复习

数据结构与八大排序算法复习
9.7k 字 82 分钟

顺序表链表什么的跳过，以下图片均盗自文末的参考文献，数据结构没图（最好是动图）简直要死。

树

度 结点的度是该节点所拥有的子树棵数。树的度是该树各节点的度的最大值。

高度 树中最大的层次数

二叉树

  1. 若根节点层次为1，则二叉树第i层最多有2i-1个节点

  2. 高度为h的二叉树中，最多有2h-1个节点

  3. 设一课二叉树叶子节点为n0，2度的节点有n2，则n0=n2-1

  4. 一课具有n个节点的完全二叉树，其高度为h=(向下取整)[log2n]+1

满二叉树 就是最底一层的节点全满的二叉树

完全二叉树 不知道怎么说，看图

二叉树遍历

  1. 先根遍历 ABC
  2. 中根遍历 BAC
  3. 后根遍历 BCA

图

完全图 无向完全图有n(n-1)/2条边，有向完全图有n(n-1)条边

度 顶点的度指的是顶点关联的边数。度为0的点为孤立点，度为1的点为悬挂点。在有向图中，点的入度指的是指向顶点的边数，出度是指离顶点的边数。

图的表示有邻接矩阵和邻接表

排序

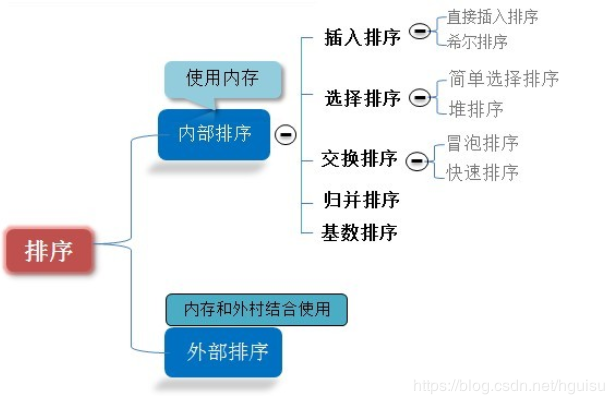
先来张图。网上说这里的八大排序是内部排序。而内部排序是指待排序列完全存放在内存中所进行的排序过程，适合不太大的元素序列。

直接插入排序

先假设数组前面n个元素是有序的，那把第n+1个元素往前面插入，直到全部元素都插入到前面，完成排序。而假设的条件“数组前面n个元素是有序的”，当n=1的时候确实是“有序”的，所以具有起始条件。而实际我实现则是：从第二个元素开始，把此元素与前一个元素比较，如果前一个元素比此元素大，则跟前一个元素交换，知道前一个元素不大于此元素为止。此过程遍历第二到最后一个元素，完成排列。

希尔排序

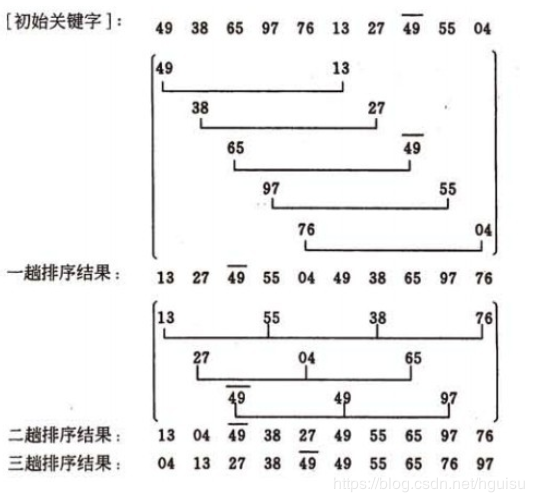
希尔排序有点难说。前面的直接插入排序，前n+1个元素是连续并排在一起的。但是希尔排序不是，他设置了一个间隔，例如隔两个，每隔两个就选择一个元素，然后在这些相互隔开的元素之间进行直接插入排序。当然，如果从第一个元素开始，间隔为2，那么只排序了三分之一的元素，所以这个过程还要从第二个，第三个元素开始。完成后，数组就有点顺序了。在然后把这个间隔减小，一般除以二，直到间隔为0.嘛，既复杂又玄学。

冒泡排序

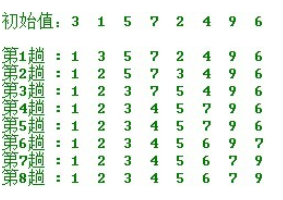
冒泡排序就好简单啦，有点像直接插入排序。第一次，从第二个元素开始，，把此元素与前一个元素比较，如果前一个元素比此元素大，则跟前一个元素交换，直到最后一个元素。这一次交换的成果是把数组最大的一个数排到数组最后面，并且数组有序了一点点。第二次也是比较交换，但是由于第一次排序，数组最后一个值是最大的，所以最后一个值不用比较，只要比较到数组长度-1个就可以了。如此类推，越到后面比较个数越少，直到只有第一第二个元素比较交换，完成排序。

快速排序

快速排序思路是在数组选择一个元素，一般就选第一个，然后把大于此元素的其他元素排到此元素的前面，大于的排到后面。这样子就根据此元素把数组分割成两个，然后把前面这个“小数组”和后面“大数组”进行递归同样的操作，直到进行递归的数组元素只有两个为止。所以这里主要问题就是怎样“把大于此元素的其他元素排到此元素的前面，大于的排到后面”？快速排序有两个指针，一个一开始在最前面，一个一开始在最后面。由于一般就选择第一个元素为分割元素，把第一个元素值取出来了，那么第一个位置空了下来，就从最后面开始往前移动后指针，直到找到一个比分割元素小元素，把这个元素移到第一个位置，然后后面就空出一个位置，又在前面找大的元素来补后面的空位，直到前后指针相等，那么两个指针所指的位置就是分割元素的位置。

直接选择排序

直接选择排序最简单了，第一次从第一个元素开始遍历一遍数组，找到最小的那个数，跟第一个数交换位置，第二次从第二个元素开始同样找最小数跟第二个元素交换，知道全部元素都被选了一遍。

堆排序

堆排序也是复杂难说。首先是一颗完全二叉树可以一一对应到一个连续的数组里，所以我们的数组一颗映射为一颗完全二叉树。经过我的观察，这里先列举几个下标关系，不过我没证明过，不过也好像是对的。例如下图第一棵树，对应，{4,1,32,16,910,14,8,7}，数组对应的下标图上已经标好。规律是：

  1. 对于下标为index的元素，他的左孩子（如果有，没有就数组越界了）下标为(index * 2) + 1

  2. 对于下标为index的元素，他的右孩子（如果有，没有就数组越界了）下标为(index * 2) + 2

  3. 对于一个有n个节点的完全二叉树，最后一个有孩子的节点的下标为(n/2)-1

堆排序自然要有堆，堆是在完全二叉树的基础上调整出来的。堆要满足

  1. 堆中的最大（最小）元素值出现在根结点（堆顶）

  2. 堆中每个父节点的元素值都大于（小于）等于其孩子结点（如果存在）

堆顶为最大值的堆为叫最大堆，最小值的叫最小堆。如果要升序，就要创建最大堆，否则创建最小堆。这里例如怎么创建最大堆呢？从最后一个有孩子的父亲节点开始，遍历到根节点。对每一个父亲节点检查其是否大于其两个孩子，否则就选择大的那个孩子跟父亲节点交换。交换之后孩子节点变了，那么以孩子节点为父节点的子树可能就不满足堆要求了，因此如果父亲节点跟子节点交换了的话，要递归检查交换的子节点。如此就创建好一个堆了。创建好堆之后，根节点就是数组最大值了，那根节点跟最后一个节点交换，最大值成功排到最后面，然后把出了最后一个值的其余元素构成的完全二叉树在构建成堆，得到第二大值，交换到倒数第二个位置，如此反复，完成排序。

归并排序

归并排序与前面的排序有点不一样，前面的排序都是在原数组本身上进行操作，最多就是创建一两个整型来临时保存数据。而归并排序需要创建一个与原等大小的新数组，空间成本更大。归并排序所做的是把数组第一个和第二个之间进行排序，第三个与第四个之间进行排序……之后1,2内部有序，3,4内部有序。然后把1,2和3,4进行合并并且排序……直到合并成一个完整的数组。归并排序的核心就是怎么合并？合并两个数组，先选择数组一的第一个值和数组二的第二个值，两值比较，小的那个值放第一位，然后取小值所在的数组的下一个值，再比较，小的放第二位如此完成合并。其实看图就会很清楚：

桶排序

桶排序需要知道排序的值的大小范围，然后把这个范围划分成n部分，即n个桶。然后遍历数组的每一个值，根据大小放进对于的桶，最后在桶内部进行排序，排序的方法可选以上的7中排序。当n越大效率越高，就像hash样的。

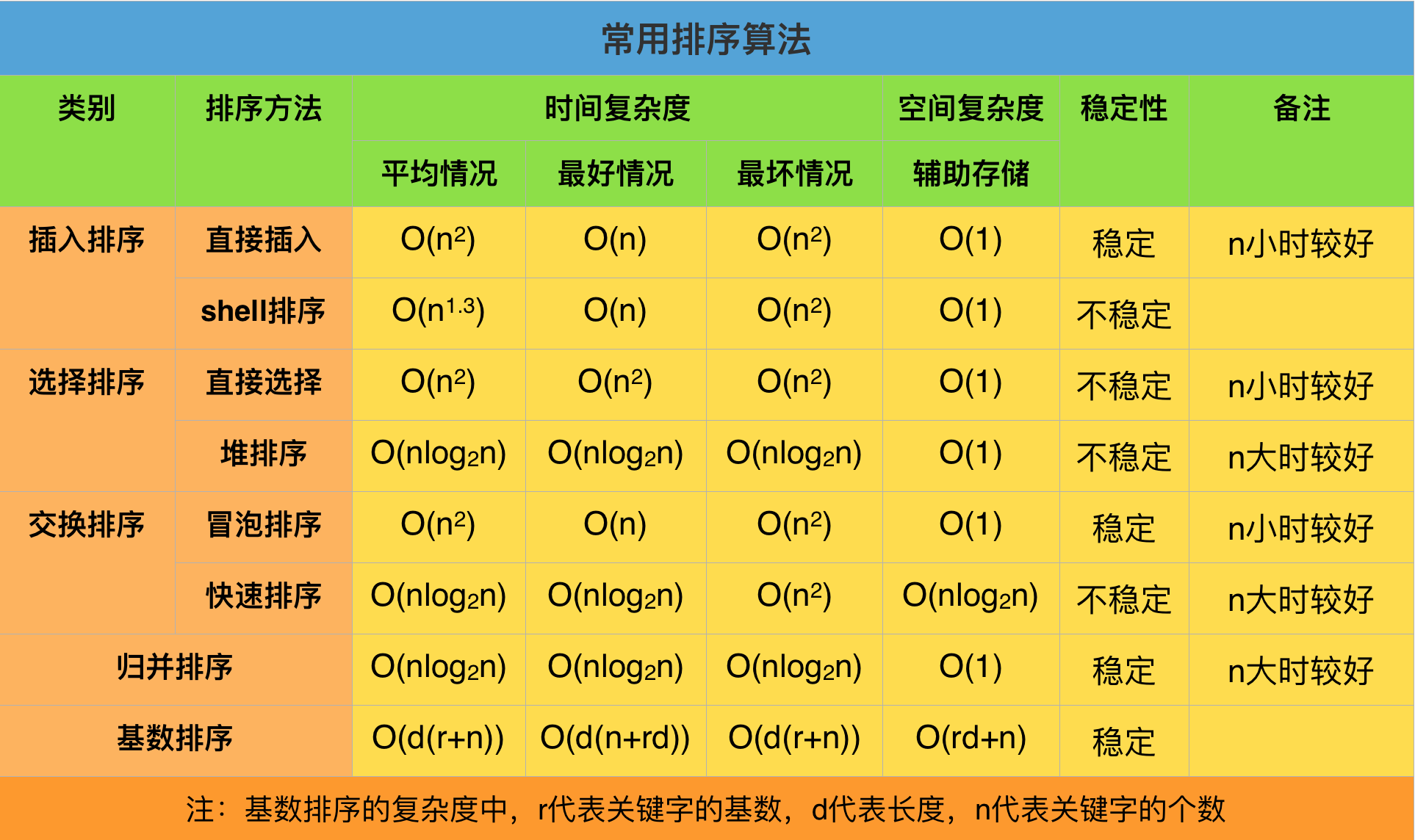
八大排序的比较

最后贴一贴代码，用java实现。虽然不保证效率，但是经过测试应该是没毛病的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
package dataStructure;

import java.util.Arrays;

/**
 * Created by cellargalaxy on 18-2-10.
 */
public class Sort {
    private static final int arrayLen = 100;
    
    public static void main(String[] args) {
        for (int i = 0; i < 10000; i++) {
            int[] ints1 = createArray();
            int[] ints2 = ints1.clone();
            Arrays.sort(ints1);
            ints2 = straightInsertionSort(ints2);
            if (!check(ints1, ints2)) {
                System.out.println("straightInsertionSort");
            }
            ints1 = createArray();
            ints2 = ints1.clone();
            Arrays.sort(ints1);
            ints2 = shellSort(ints2);
            if (!check(ints1, ints2)) {
                System.out.println("shellSort");
            }
            ints1 = createArray();
            ints2 = ints1.clone();
            Arrays.sort(ints1);
            ints2 = bubbleSort(ints2);
            if (!check(ints1, ints2)) {
                System.out.println("bubbleSort");
            }
            ints1 = createArray();
            ints2 = ints1.clone();
            Arrays.sort(ints1);
            ints2 = quicksort(ints2);
            if (!check(ints1, ints2)) {
                System.out.println("quicksort");
            }
            ints1 = createArray();
            ints2 = ints1.clone();
            Arrays.sort(ints1);
            ints2 = straightSelectSort(ints2);
            if (!check(ints1, ints2)) {
                System.out.println("straightSelectSort");
            }
            ints1 = createArray();
            ints2 = ints1.clone();
            Arrays.sort(ints1);
            ints2 = heapSort(ints2);
            if (!check(ints1, ints2)) {
                System.out.println("heapSort");
            }
            ints1 = createArray();
            ints2 = ints1.clone();
            Arrays.sort(ints1);
            ints2 = mergeSort(ints2);
            if (!check(ints1, ints2)) {
                System.out.println("mergeSort");
            }
        }
        System.out.println("over");
        
//        int[] ints1 = createArray();
//        int[] ints2 = ints1.clone();
//        String string1 = Arrays.toString(ints1);
//        String string2 = Arrays.toString(ints2);
//        System.out.println(string1);
//        System.out.println(string2);
//        System.out.println();
//        Arrays.sort(ints1);
//        ints2 = bubbleSort(ints2);
//        System.out.println(Arrays.toString(ints1));
//        System.out.println(Arrays.toString(ints2));
//        System.out.println("check: " + check(ints1, ints2));
    }
    
    /**
     * 直接插入排序
     *
     * @param ints
     * @return
     */
    public static final int[] straightInsertionSort(int[] ints) {
        for (int i = 1; i < ints.length; i++) {
            for (int j = i; j > 0; j--) {
                if (ints[j - 1] > ints[j]) {
                    int tmp = ints[j - 1];
                    ints[j - 1] = ints[j];
                    ints[j] = tmp;
                } else {
                    break;
                }
            }
        }
        return ints;
    }
    
    /**
     * 希尔排序
     *
     * @param ints
     * @return
     */
    public static final int[] shellSort(int[] ints) {
        for (int dela = ints.length; dela > 0; dela /= 2) {
            for (int k = 0; k < dela; k++) {
                for (int i = k + dela; i < ints.length; i += dela) {
                    for (int j = i; j > dela - 1; j -= dela) {
                        if (ints[j - dela] > ints[j]) {
                            int tmp = ints[j - dela];
                            ints[j - dela] = ints[j];
                            ints[j] = tmp;
                        } else {
                            break;
                        }
                    }
                }
            }
        }
        return ints;
    }
    
    
    /**
     * 冒泡排序
     *
     * @param ints
     * @return
     */
    private static final int[] bubbleSort(int[] ints) {
        for (int i = 0; i < ints.length - 1; i++) {
            for (int j = 1; j < ints.length - i; j++) {
                if (ints[j - 1] > ints[j]) {
                    int tmp = ints[j - 1];
                    ints[j - 1] = ints[j];
                    ints[j] = tmp;
                }
            }
        }
        return ints;
    }
    
    
    /**
     * 快速排序
     *
     * @param ints
     * @return
     */
    public static final int[] quicksort(int[] ints) {
        return quicksort(ints, 0, ints.length - 1);
    }
    
    private static final int[] quicksort(int[] ints, int start, int end) {
        if (end - start < 1) {
            return ints;
        }
        int tmp = ints[start];
        int i = start;
        int j = end;
        while (i < j) {
            for (; i < j; j--) {
                if (ints[j] < tmp) {
                    ints[i] = ints[j];
                    i++;
                    break;
                }
            }
            for (; i < j; i++) {
                if (tmp < ints[i]) {
                    ints[j] = ints[i];
                    j--;
                    break;
                }
            }
        }
        ints[i] = tmp;
        quicksort(ints, start, i - 1);
        quicksort(ints, i + 1, end);
        return ints;
    }
    
    /**
     * 直接选择排序
     *
     * @param ints
     * @return
     */
    public static final int[] straightSelectSort(int[] ints) {
        for (int i = 0; i < ints.length; i++) {
            int index = i;
            for (int j = i + 1; j < ints.length; j++) {
                if (ints[index] > ints[j]) {
                    index = j;
                }
            }
            int tmp = ints[i];
            ints[i] = ints[index];
            ints[index] = tmp;
        }
        return ints;
    }
    
    /**
     * 堆排序
     *
     * @param ints
     * @return
     */
    public static final int[] heapSort(int[] ints) {
        for (int without = 0; without < ints.length - 1; without++) {
            for (int i = (ints.length / 2) - 1; i > -1; i--) {
                heapSort(ints, i, without);
            }
            int tmp = ints[0];
            ints[0] = ints[ints.length - without - 1];
            ints[ints.length - without - 1] = tmp;
        }
        
        return ints;
    }
    
    private static final int[] heapSort(int[] ints, int index, int without) {
        if ((index * 2) + 1 < ints.length - without || (index * 2) + 2 < ints.length - without) {
            if ((index * 2) + 1 < ints.length - without && (index * 2) + 2 < ints.length - without && ints[(index * 2) + 1] > ints[index] && ints[(index * 2) + 2] > ints[index]) {
                if (ints[(index * 2) + 1] >= ints[(index * 2) + 2]) {
                    int tmp = ints[index];
                    ints[index] = ints[(index * 2) + 1];
                    ints[(index * 2) + 1] = tmp;
                    heapSort(ints, (index * 2) + 1, without);
                } else {
                    int tmp = ints[index];
                    ints[index] = ints[(index * 2) + 2];
                    ints[(index * 2) + 2] = tmp;
                    heapSort(ints, (index * 2) + 2, without);
                }
            }
            if ((index * 2) + 1 < ints.length - without && ints[(index * 2) + 1] > ints[index]) {
                int tmp = ints[index];
                ints[index] = ints[(index * 2) + 1];
                ints[(index * 2) + 1] = tmp;
                heapSort(ints, (index * 2) + 1, without);
            }
            if ((index * 2) + 2 < ints.length - without && ints[(index * 2) + 2] > ints[index]) {
                int tmp = ints[index];
                ints[index] = ints[(index * 2) + 2];
                ints[(index * 2) + 2] = tmp;
                heapSort(ints, (index * 2) + 2, without);
            }
        }
        return ints;
    }
    
    /**
     * 归并排序
     *
     * @param ints
     * @return
     */
    public static final int[] mergeSort(int[] ints) {
        int[] array = new int[ints.length];
        for (int len = 1; ints.length / len > 0; len *= 2) {
            for (int g = 0; g <= ints.length / len / 2; g++) {
                int start1 = g * len * 2;
                int end1 = start1 + len;
                int start2 = end1;
                int end2 = start2 + len;
                int index1 = start1;
                int index2 = start2;
                int tmp1 = mergeSort(ints, start1, start1, end1);
                int tmp2 = mergeSort(ints, start2, start2, end2);
                for (int i = start1; i < end2 && i < array.length; i++) {
                    if (tmp1 <= tmp2) {
                        array[i] = tmp1;
                        index1++;
                        tmp1 = mergeSort(ints, start1, index1, end1);
                    } else {
                        array[i] = tmp2;
                        index2++;
                        tmp2 = mergeSort(ints, start2, index2, end2);
                    }
                }
            }
            int[] tmpArray = ints;
            ints = array;
            array = tmpArray;
        }
        return ints;
    }
    
    private static final int mergeSort(int[] ints, int start, int index, int end) {
        if (index >= start && index < end && index > -1 && index < ints.length) {
            return ints[index];
        }
        return Integer.MAX_VALUE;
    }
    
    private static final boolean check(int[] ints1, int[] ints2) {
        if (ints1.length != ints2.length) {
            return false;
        }
        for (int i = 0; i < ints1.length; i++) {
            if (ints1[i] != ints2[i]) {
                return false;
            }
        }
        return true;
    }
    
    private static final int[] createArray() {
        int[] ints = new int[arrayLen];
        for (int i = 0; i < ints.length; i++) {
            ints[i] = (int) (Math.random() * 900) + 100;
        }
        return ints;
    }
}

参考文献

八大排序算法

算法
数据结构与八大排序算法复习
https://cellargalaxy.github.io/posts/算法/1.数据结构与八大排序算法复习/
作者
cellargalaxy
发布于
2018年2月11日
许可协议